A nova série de ficção científica da Netflix, intitulada O Problema dos 3 Corpos, faz referência a um dos maiores desafios da física. Mas afinal, qual é a natureza desse problema? Será algo verdadeiramente complexo para os cientistas contemporâneos? Na realidade, trata-se de um enigma que permanece sem solução há séculos e que possivelmente continuará assim indefinidamente.
O Problema dos 3 Corpos representa uma dificuldade persistente para os físicos desde os dias de Isaac Newton. Foi o próprio renomado matemático inglês que, em 1687, tentou desvendar se existe alguma possibilidade de estabilidade a longo prazo em um sistema composto por três corpos massivos, como a Terra, a Lua e o Sol.
O que é Problema dos 3 Corpos?
Na mecânica clássica, cujo ponto de partida são as leis matemáticas estabelecidas por Newton, é possível descrever facilmente as órbitas de dois corpos usando equações. Independentemente das condições iniciais dos objetos, é viável encontrar os resultados de suas posições em qualquer momento no tempo.
Esse tipo de cálculo é referido como o “Problema dos 2 Corpos” e pode ser solucionado com relativa precisão. Graças ao trabalho de Newton, os astrônomos podem prever o movimento de duas fontes gravitacionais, como uma estrela e um planeta, desde que sejam consideradas um sistema fechado, sem interferência de outros objetos.
Resolver o Problema dos 2 Corpos implica que todos os casos podem ser resolvidos. Em outras palavras, a mesma solução se aplica a qualquer sistema de dois objetos, independentemente de quais sejam. Portanto, determinar a órbita da Lua ao redor da Terra, por exemplo, não é uma tarefa difícil.
Contudo, o universo não é tão simples, e outros corpos influenciam tanto a órbita da Terra quanto a da Lua. A introdução de um terceiro corpo leva o sistema inteiro ao caos, tornando os cálculos quase impossíveis, até mesmo para supercomputadores. Não há uma solução simples para isso.
Na prática, o movimento de cada corpo depende dos outros dois, resultando em uma constante mudança no centro de massa do sistema. Por exemplo, o centro de massa do sistema Sol-Terra-Lua está localizado quase na mesma posição do Sol, mas a própria estrela oscila em torno desse centro devido à influência da massa dos outros corpos.
Toda essa “dança cósmica” faz com que o próprio centro de massa se desloque um pouco de tempos em tempos, de forma imprevisível e aparentemente aleatória, segundo os padrões humanos. Assim, não é possível medir com total precisão as condições iniciais desse sistema, e a incerteza aumenta à medida que o tempo avança.
Um problema sem solução
Sabemos que os astrônomos conhecem as órbitas dos planetas, asteroides, luas e estrelas bem o suficiente para prever suas posições em intervalos de milhares de anos, no passado ou no futuro. Então, por que o Problema dos 3 Corpos é considerado sem solução?
É que, em primeiro lugar, uma solução para o problema significaria para os físicos:
- Encontrar uma equação, ou conjunto de equações, que funcione para todos os sistemas fechados de três corpos;
- Ser capaz de prever a posição de cada corpo em qualquer momento do tempo;
- Funcionar para todas as configurações iniciais possíveis dos três corpos;
- Usar uma quantidade finita de operações matemáticas (soma, divisão, multiplicação, etc).
Quando os cientistas dizem que o Problema dos 3 Corpos não têm solução, eles querem dizer que as equações encontradas até hoje não cumprem os requisitos acima.
O que físicos fazem é buscar aproximações, com métodos que envolvem simulações de supercomputadores com grande poder de processamento. Essas soluções aproximadas podem ser calculadas atribuindo um valor numérico para cada tempo (t) dentro do intervalo desejado.
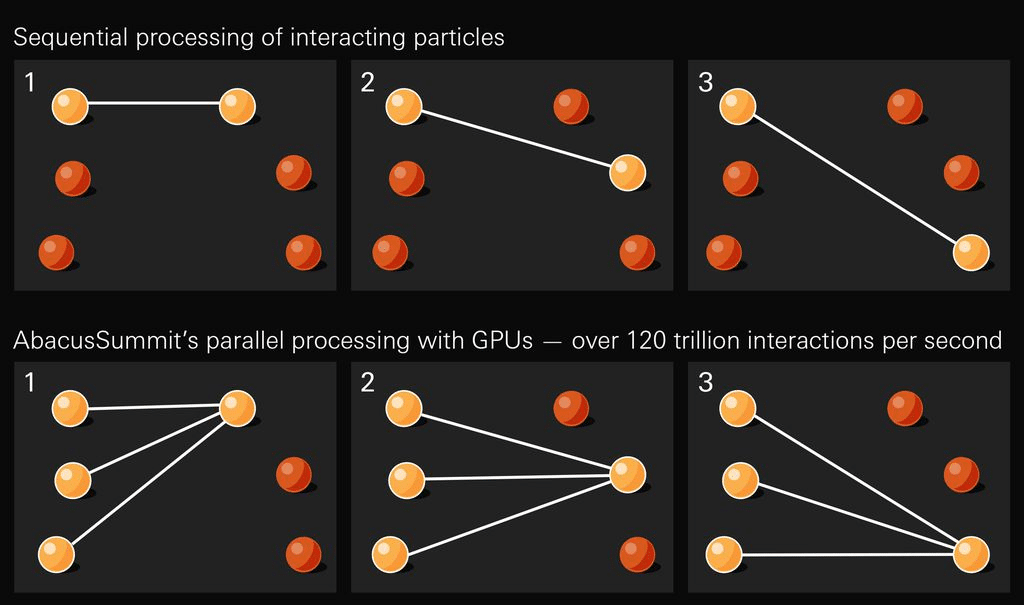
Infográfico sobre a abordagem do simulador Abacus para calcular trilhões de interações entre três partículas (Imagem: Reprodução/Lucy Reading-Ikkanda/Simons Foundation)
Por exemplo, para determinar as posições dos três corpos em t=50 segundos, deve-se calcular uma solução para cada segundo entre 0 e 50. O resultado do primeiro cálculo será usado para calcular a solução no próximo instante de tempo e assim sucessivamente.
Soluções aproximadas
Outras abordagens semelhantes incluem o conceito de “andar aleatório”, que sugere a tentativa de prever trajetórias caóticas aproveitando a imprevisibilidade a nosso favor. Analogamente ao caso de um indivíduo embriagado caminhando aleatoriamente, é viável estimar a probabilidade de sua próxima posição, considerando todas as possíveis direções de movimento.
Em sistemas de três corpos, nos quais um terceiro objeto se aproxima de um par de objetos em órbita mútua, os físicos buscam calcular as probabilidades associadas a cada velocidade possível do terceiro objeto durante essa interação. Ao combinar todas essas probabilidades, eles conseguem determinar a probabilidade geral do comportamento do sistema em qualquer ponto no tempo.
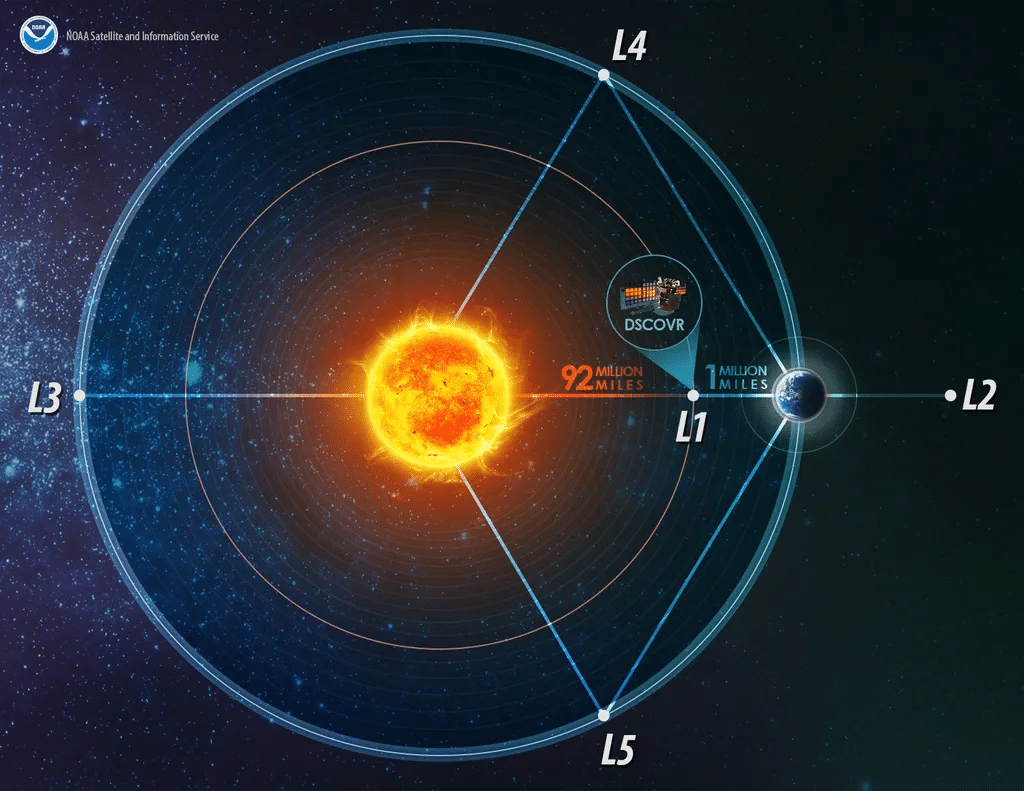
Pontos Lagrangianos surgiram de uma tentativa de resolver o problema (Imagem: Reprodução/NOAA)
O cientista suíço Leonhard Euler descobriu algumas soluções em um estudo que foi posteriormente ampliado 50 anos depois por Joseph Louis Lagrange, ítalo-francês. Eles se concentraram exclusivamente nos movimentos bidimensionais das órbitas, simplificando significativamente os cálculos.
Essa abordagem requer que um objeto no sistema em análise tenha uma massa muito menor que os outros dois, permitindo que sua influência gravitacional seja negligenciada. Através desse método, eles identificaram os “pontos neutros”, também conhecidos como Pontos de Lagrange, que são extremamente úteis para sondas e telescópios espaciais, como o James Webb.
As informações são do Canal Tech


